So a few days ago, my attention was brought to this article. It's a very straight-forward minimization problem. The crocodile/zebra spin is just fluff, the equation that needs minimized is given to the student. Find the derivative and evaluate it at zero. I can't imagine this being "too hard" for anyone who has taken Calculus 1.
I got to thinking about it, and decided to try to find a general solution. So I needed to set up the original equation. That wasn't too hard. Given width of the river, W; the distance along the bank to the target, L; and the relevant velocities (swimming, Vs; running, Vr; and flow speed, Vf (not considered in the given formula, but what the hell) the relationship is pretty easy to find. I decided to make it a function of the angle at which the crocodile swims (in my set up 0° is directly across the river, and the angle increases clockwise).
So: total time is the sum of swimming time and running time. Swimming time is easy. It is the distance across the river (at the given angle) divided by the swimming speed. Running time is a little trickier, but it works out to the absolute value of the horizontal distance to the target minus the horizontal distance covered by the swimming angle, plus drift distance. Drift distance is swimming time times flow speed. So, the total time as a function of angle is:

Taking the derivative and minimizing gives:

Check it out. It looks like the W and L don't matter. Just the ratio of velocities. But if the swimming speed is higher than the running speed plus flow speed, the result is meaningless. It turns out that even if it is close, the angle it gives is ridiculous. It isn't obvious from any of this but the function has a discontinuity cusp where
tan(θ) = L/W, and the minimization will only work to that point.
I was having a hard time showing this on paper, so I did what I always do in these situations: I wrote a program to do it for me. I used the browser-based Python interpreter at CodeSkulptor
Here it is. Use this one. Feel free to play with it.(The last I knew, CodeSkulptor doesn't work right in IE) You can change the distances and velocities. Note that negative W, Vr, and Vs are nonsense. The program can't handle negative L. Negative Vf is fine, though.
Here's a screen shot of the solution to the original problem:

Here's a screenshot of one of the weird results.

(FIX: there was a bug in my drift calculation when I took that. The minimum time will never have the crocodile landing upstream of the target. It is fixed in the final version)
Later,
UPDATE: I changed the color scheme for better contrast, and fiddled with the scale and offset to show that the discontinuity cusp is still there in the original problem

The
Later,
UPDATE #2: Okay, I worked out the relationship that determines the angle where the

The quadratic formula technically has '+ or -', but the '-' case can be discounted because that result is outside of the range the problem makes sense for, [0°,90°). If flow speed (Vf) is zero, this simplifies to cos(θ) = W/√W²+L², which equates to tan(θ) = (L/W).
Aside from the initial minimization that made me aware of the
So
Later,
UPDATE #(Again? WTF?): It occurred to me that I was using "discontinuity" wrong. The function is not discontinuous, it is continuous but not differentiable at the cusp. So, I have corrected the post.
Note to self: Do not use Blogger's "compose" mode. It adds a ton of weird, unnecessary html to the post.
Later,
UPDATE #(Seriously, what the hell is wrong with you?): I couldn't help thinking about the cases where the minimization doesn't apply. It really isn't that mysterious. As Vs approaches (or equals) Vr+Vf, the resulting θ would be beyond the cusp. which means that it doesn't apply. The total time function follows a different curve to the right and left of the cusp. There is actually a discontinuity in the curve. 1/cos(θ) → infinity as θ → 90°. Of course, the cusp usually comes before you get close to the discontinuity, so the minimum time will always be between 0° and the cusp. Well, if the flow speed is high, the cusp calculation can be outside the (-90°, 90°) range. but in that case the function is differentiable across that entire range, and the minimization applies. This got me wondering why my program didn't work for L < 0. It should have been obvious. I was only evaluating the equation for θ in [0°, 90°). If L < 0, θ < 0°. Once I fixed that to (-90°, 90°), I had to put an absolute value on the cos(θ) in the swim time evaluation (even if the angle at which the crocodile swims across the river is negative, the time it takes is still positive). I changed my graphics to reflect the change. So, once again, here is
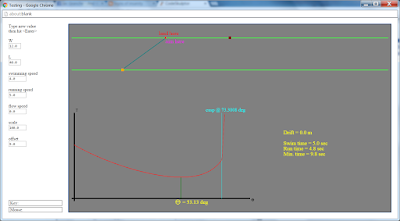
And the obligatory screenshot:

Later,
UPDATE #(Holy Shit! You're still on about this?): I couldn't stop fiddling with the program. I added Try-Except statements to the input handlers so that entering bad values wouldn't crash the program. Try it. I also made some corrections to the graph display. So here is the latest 'final' version.
And a screenshot:

Later,




