Ugh. This thing again.

I know I've done this before, but this stupid thing keeps showing up in my feeds. And it pisses me off to no end.

What happened to that little square of area?
It isn't missing. IT ISN'T MISSING!
There's a trick here.
It relies on the way the eye handles those colors and the zoom level.

Let's take a closer look at the left triangle:

And there it is. The triangles aren't similar.
The Red triangle is 7 units wide and 3 units tall, so the slope ≈ 0.4286
The Orange triangle is 12 units wide and 5 units tall, so the slope is ≈ 0.4167
When they are arranged this way, there's a slight concavity to the figure.

Now let's look at the re-arranged triangle on the right:

Now there's a slight convexity.
This figure has the area of the first figure minus the "missing" chunk PLUS the area of the original concavity PLUS the area of the convexity.
Guess what the area of the concavity plus the convexity equals.

Later,

This was not supposed to be a stream-of-conciousness rant

When I decided to make a new post here, I did actually have a thesis in mind. However, while planning it I thought of several side-topics that I felt were just as important. So I gave up and just started typing. So, beware of wildly unpredictable topic shifts. Also, this is going to be an "As I understand things/My opinion" rant, so I probably (probably) won't be looking up formal definitions of things.

Anyway:
I recently read a statement along the lines of "The Scientific Method is the only way to really know anything." I've seen this sort of thing before and have a couple of issues with it.

One: I don't think the scientific method is deserving of capitalization as if it's some kind of special "thing" in it's own right (Ha! quotations for emphasis!) It's just a process that is important to critical thinking.

Two: The statement isn't actually true. There is really only one way to know something with 100% certainty: valid mathematical or logical proof ("valid" here includes that the initial axioms are true, which should lead to a chain of proofs all the way back to first principles AND that the proof has been verified/error-checked). Everything else is about how confident you can be that what you believe is correct.
Note: "Confidence" here is not about personal confidence. For example: you may be 100% confident that there are thousands of spiders crawling all over you, but there is always the possibility that you are hallucinating.
Also note: "I am not hallucinating" is an unspoken axiom for basically all observations and may not be true, which is why independent verification/duplication of results is necessary.
The other thing about the statement is that it is an over-simplification. There's more to it. Specifically: the accuracy of your measurements. The quote "Messen is wissen [to measure is to know]" is attributed to Georg Ohm; other people (including Lord Kelvin of absoulte zero temperature fame) have said very similar things. And it is mostly true. If you can't measure a thing, you can't know anything about it (not even that it really exists). But that knowledge only extends as far as the accuracy of the measurements. Which is why people bringing up statements from many (sometimes hundreds of) years ago bugs the shit out of me. I am an instrumentation tech. I will always ask "How much error is in that measurement?"

On to a related topic:
I also often see the statement "You can't prove a negative" (usually from people explaining why something's existence is astronomically unlikely. People who are defending that thing's existance usually phrase it "Absence of evidence is not evidence of absence").
Both are oversimplified. "It is not currently raining here." is a pretty obvious falsification of the first (with the "not hallucinating" caveat. Come on, be reasonable). "When I look in front of me, I do not see a person standing there. Therefore, there is not a person standing in front of me." is a good falsification of the second (again, be reasonable).
This may seem like nitpicking. Of course both are referring to a thing that can't be observed/measured. But those statements almost never specify that, and are presented as absolute truths. The actual statement should be "If you can't measure a thing, you can't say anything about its existance." If you say "There is wifi here." I can't say you are right or wrong if I don't have a smartphone (or some other wifi capable device or a signal strength meter) because I can't measure the signal without one. But keep in mind that indirect measurements can also be made. Things that exist have consequences on things around them. Making predictions (we're back on the scientific method) about things that can't directly be observed is asking "If this hypothesis is true, what would that mean for or do to the things around it?" If the answer is "nothing" then that thing might as well not exist.

Which brings up atheism vs theism

If you insist on a whimsical entity that hides all evidence of its own existence, then I'm going to ask you to disprove the Invisible Pink Unicorn, Russell's Teapot, and Last Thursdayism. If you are specifically xian, I'm going to ask you: What changed? What happened to "as it was in the beginning, is now, and ever shall be"?

You know what? I'm not gonna go off on this again. All I'm going to say about religion is this: They can't all be right. But they certainly can all be wrong.

Later,

More Soup

 I made some Tom Kha Gai today.

Being me, I couldn't find a recipe that looked quite right, so I cobbled several togather.
It came out pretty good.  The only changes I'd make are:  more chilis, more curry paste, more lime juice, add some salt.

So here's my recipe for Tom Kha Gai:

Ingredients:
    4T coconut oil, divided
    1 med. onion, roughly chopped, divided
    3 cloves garlic, chopped
    several Thai chilis, halved (more or less depending on desired spiciness)
    3 ¼-inch slices galangal or ginger
    1  stalk lemongrass, crushed with the flat a knife and cut into 2-inch pieces
    2 teaspoons red Thai curry paste (more or less depending on desired spiciness)
    1 32 oz box + 1 14.5 oz can chicken stock
    4-5 kaffir lime leaves
    2 13.5 oz cans coconut milk
    1-2 lb chicken thighs, sliced
    2 c white mushrooms, quartered
    1 red bell peper, chopped
    1 c halved cherry tomatoed
    1/4 head cabbage, roughly chopped
    3T fish sauce (more or less to taste)
    1/4 c lime juice (more or less to taste)

Process:
    Heat 2T oil in a saucepan (large enough to hold the chicken stock easily).  Add 1/2 of the onion, the garlic, the chilis, the galangal (or ginger), the lemongrass, and the curry paste.
    Saute until the onions soften (around 5 minutes).  Add the chicken stock.  Bring to a boil, then reduce to a simmer.  Add the kaffir lime leaves. Simmer uncovered for 45 minutes (or so).

    Strain broth and discard solids (I strained it into another pot to simplify things).  Add the coconut milk, chicken, mushrooms, and cherry tomatoes.  Bring to boil again, then reduce to a simmer. Simmer uncovered until the chicken is fully cooked.
    In the meantime, heat the remaining oil and saute the other 1/2 onion and the bell pepper until the onions are translucent (around 10 minutes).  Add to the stock.  

    Once the chicken is cooked, add the cabbage, fish sauce, and lime juice.  Continue to simmer until cabbage reaches desired softness.

    Serve hot.

I didn't have any garnish, but cilanto and sliced green onion are popular.

Later,

Girls' Last Tour

Okay, I want to get this out of the way immediately:
THIS ANIME WILL MAKE YOU SAD!
Seriously. It should have a legally required warning. If it doesn't make you sad, then you are a monster and I do not want to know you.

It is also one of the best things I have seen in a long, long time. Not just anime. Anything.

It is available on Amazon Prime Video (link in title). This is the synopsis:
"In a future where most of humanity has perished, two young girls explore the ruins of civilization looking for food and fuel."
That's the entire plot. By all rights, I should think this was boring as hell, but it never was. Even watching it the second time, when I knew exactly what was coming.

The two protagonists, Chito and Yuuri, are immediately engaging, just driving through the dark, barely talking. That, combined with the weird abandoned-industrial setting, had me invested in the story from the get-go.

Chito (Chi) is thoughtful and bookish (also easily irritated by Yuuri). The (very) occasional flashbacks and dream sequences are from her PoV. She keeps a journal, even though she knows no one will ever read it.
Yuuri (Yuu) is living on Zen time (there is only today and there never will be anything except today). Sometimes she briefly wonders about the past, but never more than as idle curiosity. Same with the future, but even more so. She can barely read or write, but isn't dumb.
Both of them are well aware of their situation. Neither seems deeply bothered by it.

There are some nice, touching moments. There are some really funny moments. There are some brief existential discussions. But it's still just these two (mostly - they do meet some other people) driving around aimlessly (they went into the factory in the first episode on Yuu's whim). Their only destination is "higher" (it's a Layered City) , and even the search for food/fuel doesn't seem that urgent to them, although they are always aware of their limited supplies (and of what happens if they run out).

There is a lot more to say about it (and really, no one is going to read this - spoilers aren't an issue), but I don't want to go deep into specifics right now.

If you don't mind a sad story, this is a good one that I cannot recommend strongly enough.

Later,

UPDATE: One sort-of negative thing: I'm not sure my issue with heights counts as even mild acrophobia, but oh-someone's-god did the third and eighth episodes set it off.

river math problem

So a few days ago, my attention was brought to this article. It's a very straight-forward minimization problem. The crocodile/zebra spin is just fluff, the equation that needs minimized is given to the student. Find the derivative and evaluate it at zero. I can't imagine this being "too hard" for anyone who has taken Calculus 1.

I got to thinking about it, and decided to try to find a general solution. So I needed to set up the original equation. That wasn't too hard. Given width of the river, W; the distance along the bank to the target, L; and the relevant velocities (swimming, V_s; running, V_r; and flow speed, V_f (not considered in the given formula, but what the hell) the relationship is pretty easy to find. I decided to make it a function of the angle at which the crocodile swims (in my set up 0° is directly across the river, and the angle increases clockwise).

So: total time is the sum of swimming time and running time. Swimming time is easy. It is the distance across the river (at the given angle) divided by the swimming speed. Running time is a little trickier, but it works out to the absolute value of the horizontal distance to the target minus the horizontal distance covered by the swimming angle, plus drift distance. Drift distance is swimming time times flow speed. So, the total time as a function of angle is:

Taking the derivative and minimizing gives:

Check it out. It looks like the W and L don't matter. Just the ratio of velocities. But if the swimming speed is higher than the running speed plus flow speed, the result is meaningless. It turns out that even if it is close, the angle it gives is ridiculous. It isn't obvious from any of this but the function has a discontinuity cusp where
tan(θ) = L/W, and the minimization will only work to that point.

I was having a hard time showing this on paper, so I did what I always do in these situations: I wrote a program to do it for me. I used the browser-based Python interpreter at CodeSkulptor

Here it is. Use this one. Feel free to play with it.(The last I knew, CodeSkulptor doesn't work right in IE) You can change the distances and velocities. Note that negative W, V_r, and V_s are nonsense. The program can't handle negative L. Negative V_f is fine, though.

Here's a screen shot of the solution to the original problem:


Here's a screenshot of one of the weird results.


(FIX: there was a bug in my drift calculation when I took that. The minimum time will never have the crocodile landing upstream of the target. It is fixed in the final version)

Later,

UPDATE: I changed the color scheme for better contrast, and fiddled with the scale and offset to show that the discontinuity cusp is still there in the original problem

The discontinuity cusp is at θ = atan(L/W) if there is no drift. Adding drift changes the angle at which the crocodile would swim directly to the target. That is where the run time calculation (the absolute value term in the total time equation) is zero. I'm not sure I can simplify it to a relationship. I can see that V_r divides out, and the angle depends on W, L, V_s, and V_f. Maybe I'll work on it more this weekend.

Later,

UPDATE #2: Okay, I worked out the relationship that determines the angle where the discontinuity cusp is. It is a horribly messy quadratic:

The quadratic formula technically has '+ or -', but the '-' case can be discounted because that result is outside of the range the problem makes sense for, [0°,90°). If flow speed (V_f) is zero, this simplifies to cos(θ) = W/√W²+L², which equates to tan(θ) = (L/W).

Aside from the initial minimization that made me aware of the discontinuity cusp , this has all been algebra and trigonometry. Messy, sure, but not actually hard.

So here Use this one. is the final version of my program. Here is a screenshot of the original problem, showing the location of the discontinuity cusp:

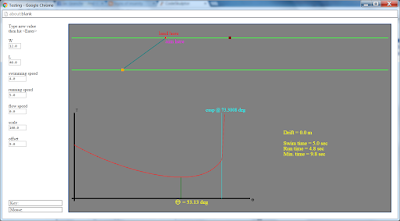
Later,

UPDATE #(Again? WTF?): It occurred to me that I was using "discontinuity" wrong. The function is not discontinuous, it is continuous but not differentiable at the cusp. So, I have corrected the post.

Note to self: Do not use Blogger's "compose" mode. It adds a ton of weird, unnecessary html to the post.

Later,

UPDATE #(Seriously, what the hell is wrong with you?): I couldn't help thinking about the cases where the minimization doesn't apply. It really isn't that mysterious. As V_s approaches (or equals) V_r+V_f, the resulting θ would be beyond the cusp. which means that it doesn't apply. The total time function follows a different curve to the right and left of the cusp. There is actually a discontinuity in the curve. 1/cos(θ) → infinity as θ → 90°. Of course, the cusp usually comes before you get close to the discontinuity, so the minimum time will always be between 0° and the cusp. Well, if the flow speed is high, the cusp calculation can be outside the (-90°, 90°) range. but in that case the function is differentiable across that entire range, and the minimization applies. This got me wondering why my program didn't work for L < 0. It should have been obvious. I was only evaluating the equation for θ in [0°, 90°). If L < 0, θ < 0°. Once I fixed that to (-90°, 90°), I had to put an absolute value on the cos(θ) in the swim time evaluation (even if the angle at which the crocodile swims across the river is negative, the time it takes is still positive). I changed my graphics to reflect the change. So, once again, here is the actual, final version Use this one.
And the obligatory screenshot:

Later,

UPDATE #(Holy Shit! You're still on about this?): I couldn't stop fiddling with the program. I added Try-Except statements to the input handlers so that entering bad values wouldn't crash the program. Try it. I also made some corrections to the graph display. So here is the latest 'final' version.
And a screenshot:

Later,

Cherry Marshamallows

This is the sort of thing that happens when I get bored:

The pink mess in the bowl is a previous batch that I left too close to a hot oven, and melted into a gooey pile.  Jac suggests making Rice Krispy treats with it.  I'll probably do that.

The plate on the right has the finished marshmallows from the second batch.  They are dusted in powdered sugar to keep them from sticking together.  They are actually purple, as can be seen on the exposed half-marshmallow.  These are awesome in hot chocolate or s'mores.

The plate on the left has the Frankensteinian remnants, and a few salvaged pieces from the first batch, dipped in chocolate.

The reason the first batch is pink, and the second purple is a change in the recipe. The original recipe called for cherry extract and a few drops of red food coloring.  I used the last of my cherry extract making it.  When I decided to make another batch, I went to the store to get more, but there wasn't any.  So I got cherry juice and substituted it for the water in the original.  I wasn't sure it would work, but I'm pretty happy with the results.  Next time I'll add some extract, too, though.  The cherry flavor is pretty subtle with just the juice.

So here's my (revised) recipe for Cherry Marshmallows.

Equipment:
   Electric mixer

   Whisk

   Rubber scraper
   Heavy-bottomed 2-qt saucepan

   Candy thermometer
   Medium mixing bowl (I prefer one with straight sides)

   Small microwave-safe bowl

   Baking dish (I used an 11"x7" brownie pan)

   Cling wrap

   Chef's knife

Ingredients:

   2 lg. egg whites, at room temperature

   1 c. cherry juice (I used black-cherry juice, I think that's why they're purple)

   3 envelopes unflavored gelatin

   2 c. granulated sugar

   1/2 c. light corn syrup

   1/4 t. salt
   1 t. cherry extract (or more for a stronger flavor)

   powdered sugar

   non-stick spray

Process:

   Line the baking dish with cling wrap and spray with non-stick spray.
   Mix gelatin and 1/2 c cherry juice in microwave safe bowl and set aside.

   Put egg whites in mixing bowl and set aside.

   Mix remaining 1/2 c juice, granulated sugar, corn syrup, and salt in saucepan.

   Heat on med-high.  Stir until sugar is dissolved.  Insert thermometer.

   Heat to 260°F.  Note - when it starts to boil, it will make a mess if the saucepan is

   too small.

   Watch the thermometer.  When the sugar mixture gets to about 240°F, start 

   beating the egg whites.

   They should form stiff peaks about the time the sugar gets to 260°.
   Microwave gelatin on high for 20 seconds.  Stir to fully liquefy.

   Whisk gelatin into sugar mixture.  Note - this will cause a lot of steam.  Be careful.

   Slowly pour sugar/gelatin mixture into egg whites while beating on low.  Not too

   slowly, if the sugar cools it will harden.

   Add cherry extract and gradually increase speed to med-high.
   Beat until very thick and glossy, 8 to 10 minutes.

   Pour into prepared dish.  Let sit at least 8 hours to allow gelatin to set.

   Dust (liberally) a cutting board with powdered sugar.  Flip marshmallow onto

   board and remove pan and cling wrap.  Dust marshmallow with powdered sugar.

   Cut into strips (then cubes) with chef's knife.  Dust knife with powdered sugar as it

   gets sticky. And it will.  

   Dust cubes with powdered sugar, then brush off excess.

Later, 

Quote button

A long time ago, shortly after I added the "new quote" button on my random quote generator, Tom said it would be better to have the button above the quote so that it didn't move every time the quote length changed.  I didn't really care, so I never bothered.  Until just now.

Later,